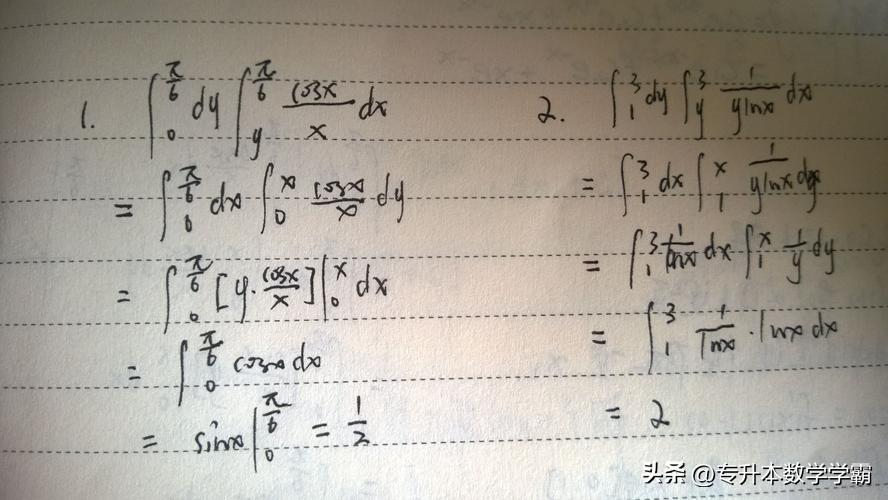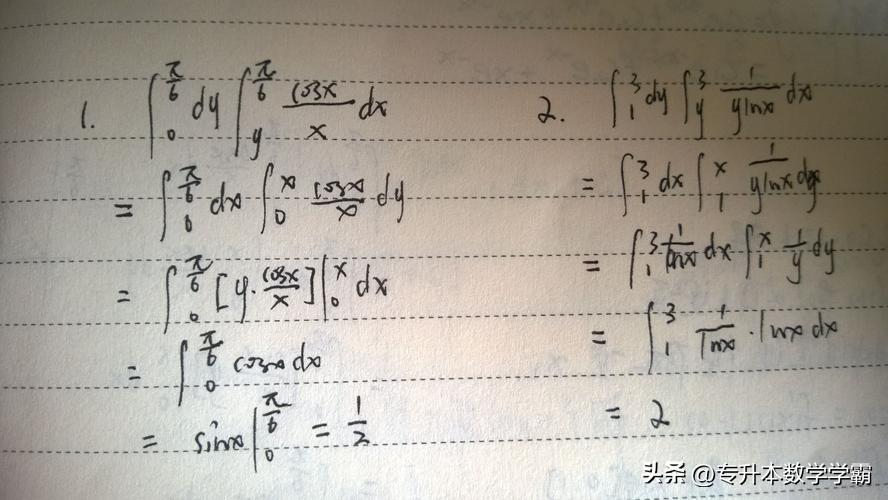二重积分交换积分次序的方法

二重积分的交换积分次序

在高等数学中，二重积分是一种计算面积和体积的方法。在计算二重积分时，我们需要选择一个合适的积分次序，以便简化计算。本文将介绍如何交换二重积分的积分次序。

一、定义与性质

二重积分是计算二维平面上的面积问题，其定义如下：

∫∫D f(x,y) dxdy

其中，D是一个二维平面上的有界区域，f(x,y)是一个定义在D上的可积函数。

在进行二重积分时，我们需要选择一个合适的积分次序，以便简化计算。常用的积分次序是先对x积分，再对y积分，即“先x后y”。但是，有时候我们需要交换积分次序，以便更好地解决问题。交换积分次序的方法是基于以下性质的：

性质1：交换积分次序后，被积函数f(x,y)在新的积分次序下变为f(y,x)。

性质2：交换积分次序后，积分区域D在新的积分次序下变为一个新的区域D'。

二、交换积分次序的方法

交换二重积分的积分次序需要遵循以下步骤：

步骤1：画出积分区域D的图形。

步骤2：根据图形确定新的积分次序，例如“先y后x”或“先x后y”。

步骤3：根据性质1和性质2，将原来的二重积分转换为新的二重积分形式。例如，原来的二重积分是∫∫D f(x,y) dxdy，交换积分次序后变为∫∫D' f(y,x) dydx。

步骤4：根据新的二重积分形式，计算新的积分值。如果计算过程中出现新的区域D''，则需要继续交换积分次序，直到得到最终的积分值。

三、举例说明

下面举一个具体的例子来说明如何交换二重积分的积分次序。

例题：计算二重积分 ∫∫D (x + y) dxdy，其中D是由曲线y = x^2和直线y = 1围成的区域。

解：首先画出区域D的图形（图略）。由于区域D的图形关于直线y = x对称，我们可以选择“先x后y”或“先y后x”的积分次序。为了简化计算，我们选择“先y后x”的积分次序。

根据性质1和性质2，将原来的二重积分转换为新的二重积分形式：

∫(1 → 1) dy ∫(y^2 → 1) (x + y) dx = ∫(1 → 1) dy (xy + x^2/2) | (y^2 → 1)
= ∫(1 → 1) (y + y^3/2 + 1/2 - y^5/2) dy = (y^2/2 + y^4/4 + y/2 - y^6/6) | (1 → 1) = 1/4。