圆周率怎么算的呢（竟然还可以这样计算圆周率π）

什么是圆周率π？

如何用蒙特卡洛法来计算圆周率？

圆周率π

圆周率用希腊字母π（读作[paɪ]）表示，是一个常数（约等于3.141592654），是代表圆周长和直径的比值。

它是一个无理数，即无限不循环小数。

圆周率是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。

π也等于圆形之面积与半径平方之比，是精确计算圆周长、圆面积、球体积等几何形状的关键值。

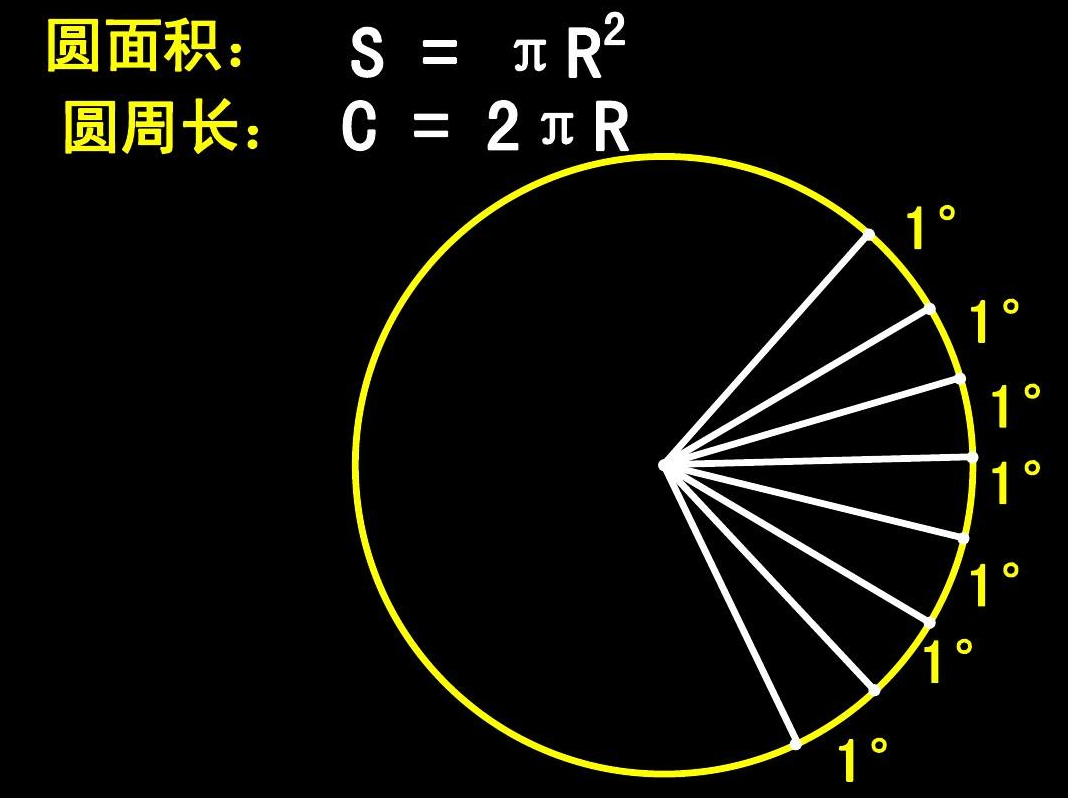
在分析学里，π可以严格地定义为满足sinx=0的最小正数x。

在日常生活中，通常都用3.14代表圆周率去进行近似计算。而用九位小数3.141592654便足以应付一般计算。

即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百个位。

披萨

你喜欢吃披萨吗？

有没有注意到，披萨一般都是圆的，而包装披萨的盒子却是正方形的。

类似这样：

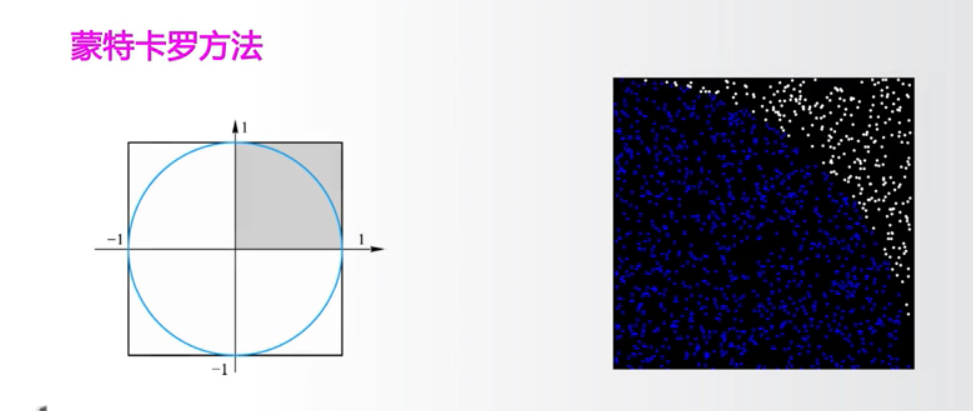
我们选取1/4，然后随机撒芝麻在上面，假设芝麻足够多。

上图正方形的面积是多少？

2*2=4

上图圆的面积是多少？

π*1*1=π

正方形面积取右上角1/4为1，圆面积取右上角1/4为π/4。

假设落在1/4圆的芝麻数是x，落在1/4正方形的芝麻数是y。

那么x:y=π/4:1。

我们用计算机随机生成大量数据，模拟落在圆和正方形中的数量，不就可以计算π了吗？

蒙特卡洛法来计算圆周率

上述算法是由蒙特卡洛提出来的，也称为蒙特卡洛方法（Monte Carlo method）。

其理论基础是大数定律。

大数定律

大数定律是描述相当多次数重复试验的结果的定律，在大数定理的保证下:

利用事件发生的频率作为事件发生的概率的近似值。

只要设计一个随机试验，使一个事件的概率与某未知数有关，然后通过重复试验，以频率近似值表示概率，即可求得该未知数的近似值。

样本数量越多，其平均就越趋近于真实值。

此种方法可以求解微分方程，求多重积分，求特征值等。

概率论历史上第一个极限定理属于伯努利，后人称之为“大数定律”。

伯努利家族星光闪耀、人才济济的现象，数百年来一直受到人们的赞颂，也给人们一个深刻的启示：家庭的“优势积累”，优秀人才成长的摇篮。

概率论中讨论随机变量序列的算术平均值向随机变量各数学期望的算术平均值收敛的定律。

在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。

通俗地说，这个定理就是，在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。偶然中包含着某种必然。

大数定律分为弱大数定律和强大数定律。

Python代码实现

从上面推断可以得出， 蒙特卡洛法计算圆周率的精度和数据个数有关，数据量越大，圆周率越精确。

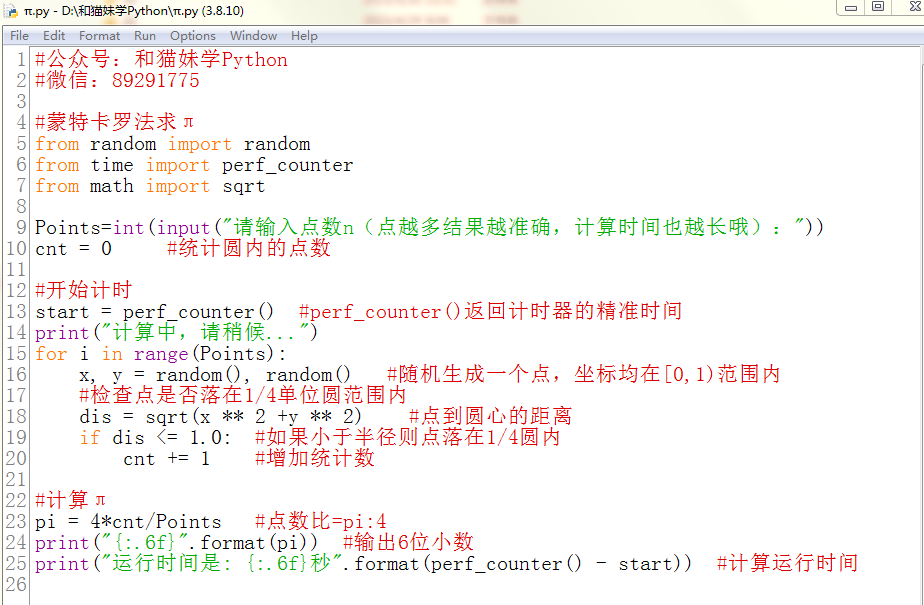
测试结果：